Beschreibung des Datensatzes
Beim Iris Datensatz, der hier im CSV-Format vorliegt,
handelt es sich um einen Datensatz mit 150 Beobachtungen von 4 Attributen von Schwertlilien.
Gemessen wurden dabei jeweils die Breite und die Länge des Kelchblatts (Sepalum) sowie des
Kronblatts (Petalum) in Zentimeter.
Des weiteren ist für jeden Datensatz die Art der Schwertlilie (Iris setosa, Iris virginica oder Iris versicolor) angegeben.
Für jede Schwertlilienart liegen 50 Datensätze vor. (Eine genauere Beschreibung kann auf
Wikipedia nachgelesen werden.)
Dieser Datensatz wird beispielsweise in der Clusteranalyse bzw. in der Mustererkennung als Testdatensatz herangezogen,
um aufgrund der gemessenen Attribute die Art der Schwertlilie automatisch zu erkennen. Der Datensatz eignet sich gerade
deshalb so gut, weil eine Schwertlilienart aufgrund der Messungen sehr gut identifiziert werden kann, während
die beiden anderen Arten überschneidende Wertebereiche in jeder Eigenschaft aufweisen. Außerdem ist eine Darstellung aller
Informationen im dreidimensionalen Datenraum (z. B. mit einem 3D-Scatterplot) nicht mehr möglich, weshalb der Datensatz auch
in der Informationsvisualisierung zur Anwendung kommt, weil hier Daten ohne inhärenten Raumbezug analysiert werden.
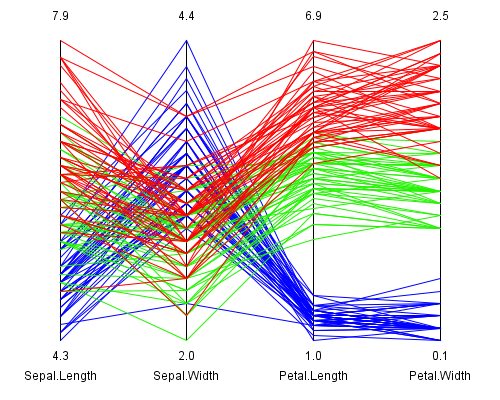
Abbildung 1: Darstellung des Iris-Datensatzes mittels Parallelen Koordinaten
Diese Darstellung mit Hilfe der Parallelen Koordinaten zeigt die 4 Messungen eingefärbt nach der Art der Schwertlilien.
Die blauen Daten repräsentieren Iris setosa, die grünen Iris versicolor und die roten Linien sind
Messungen von Iris virginica.
Daraus kann man erkennen, dass mit Hilfe der Werte der Länge und Breite des Kronblatts (= 3. und 4. Messung)
die blau eingezeichneten Iris setosa Daten klar vom Rest der Daten unterschieden werden können.
Der Datensatz wird auch von Programmen wie R
zur Verfügung gestellt. In R muss in der
Befehlszeile lediglich iris
eingegeben werden und der Datensatz wird ausgegeben.
Clusteranalyse
In der Clusteranalyse versucht man automatisiert Gruppen, sogenannte Cluster, in den Daten zu finden. Da man beim Iris Datensatz aufgrund der Messungen die drei Lilienarten unterscheiden will, wird in diesem Beispiel ein k means Cluster Algorithmus auf den Messungen ausgeführt, wobei 3 Clusterzentren angegeben werden. (Näheres zum k means clustering kann hier nachgelesen werden.)
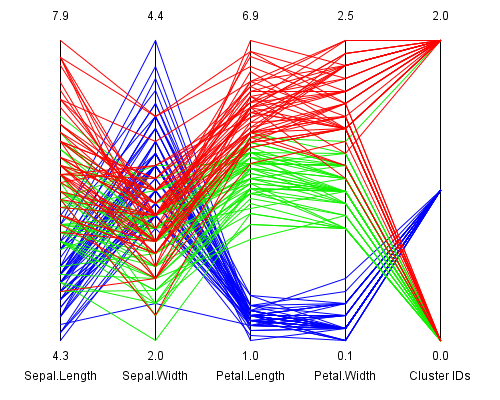
Abbildung 2: K means clustering des Iris Datensatzes
In obiger Abbildung wurde zu den 4 Messungen eine fünfte Dimension, die ermittelten Cluster-Zuordnungen,
hinzugefügt. Die Einfärbung der Daten wurde wie in Abbildung 1 gleich behalten.
Man kann daraus ersehen, dass die blauen Daten eindeutig dem Cluster mit der ID 1 zugeordnet werden, während
sich die Daten der beiden anderen Lilienarten auf zwei Cluster aufteilen. Cluster 0 repräsentiert mehrheitlich
grüne Daten (Iris versicolor) während der Cluster 2 hauptsächlich rote Daten (Iris virginica)
enthält. Dennoch wird keine perfekte Zuordnung nach Lilienart erreicht.
Der Datensatz mit dem Clusterergebnis aus Abbildung 2 steht
hier zur Verfügung.
Es ist aber auch anzumerken, dass der k means Clusteralgorithmus sehr stark von der Wahl der
anfänglichen Clusterzentren abhängig ist. Meist werden zu Beginn k zufällige Datenpunkte als
Clusterzentren gewählt. Unterschiedliche Ausgangseinstellungen können danach aber zu
signifikant anderen Gruppenaufteilungen führen. In Abbildung 3 sieht man ein Clusterergebnis,
das keine der drei Lilienarten perfekt in eine Gruppe zusammenfasst.
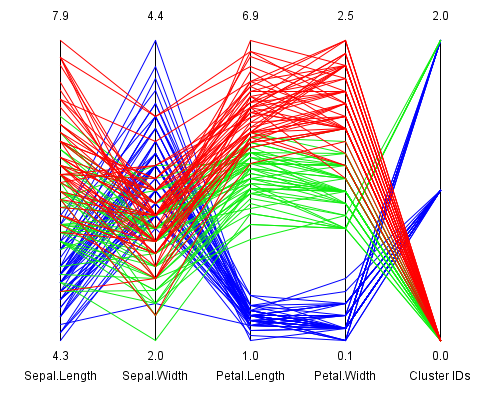
Abbildung 3: Alternatives k means Clusterergebnis
Dimensionsreduktion mittels PCA
Mit Hilfe der Principal Component Analysis (PCA - Hauptkomponenentenanalyse) kann der Großteil der Varianz in den Daten in wenigen Dimensionen dargestellt werden. Somit ist es möglich die Daten auf 2 "künstlichen" Attributen abzubilden, welche Linearkombinationen der originalen Dimensionen sind. Und daraus lässt sich mit Hilfe eines 2D Scatterplots erkennen, dass sich lediglich zwei Gruppen an Datenwerten trennen lassen. Bildet man die 4 Messungen des Iris Datensatzes auf zwei solche "künstliche" Dimensionen, sogenannte Hauptkomponenten oder Principal Components, ab, so werden mit diesen 97,8 % der Varianz der Daten repräsentiert. (Näheres zum Thema PCA kann hier nachgelesen werden.)

Abbildung 4: Ersten beiden Hauptkomponenten des Iris Datensatzes
Der Datensatz mit den ersten beiden Hauptkomponenten steht hier zur Verfügung.
Referenzen
Der Iris-Datensatz wird derzeit auf folgenden Seiten verwendet:
|
|
Visualisierung - Statistische Analysen mit Parallelen Koordinaten
(Wintersemester 2005/06) |