Zum Download des Programms
| « k means Clustering | Hauptkomponentenanalyse (PCA) » |
Mahalanobis und robuste Distanz
Die Mahalanobis Distanz gibt für jeden Datenpunkt an,
wie weit dieser vom Zentrum der Daten (unter Berücksichtigung der Streuung) entfernt ist.
Ein ausführliches Beispiel, das die Funktionalität der Mahalanobis Distanz illustriert,
kann man hier nachlesen.
Sie wird wie folgt berechnet:
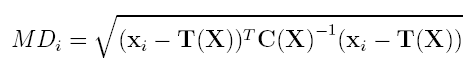
C(X) repräsentiert die Kovarianzmatrix und T(X) das komponentenweise arithmetische Mittel. Da sowohl
das arithmetische Mittel als auch die Kovarianzmatrix durch Ausreißer stark beeinflusst werden kann,
kann eine robuste Schätzung der Lokation (T(X)) und der Streuung (C(X)) verwendet werden,
um eine robuste Distanz zu ermitteln.
Um den Unterschied zwischen der Mahalanobis und der robusten Distanz aufzuzeigen wurde der künstliche
Datensatz von Hawkins, Bradu, and Kass (1984) verwendet. Der Datensatz besteht aus
75 Beobachtungen, von denen die ersten 14 Ausreißer sind. Dies ist in folgender Abbildung zu erkennen.
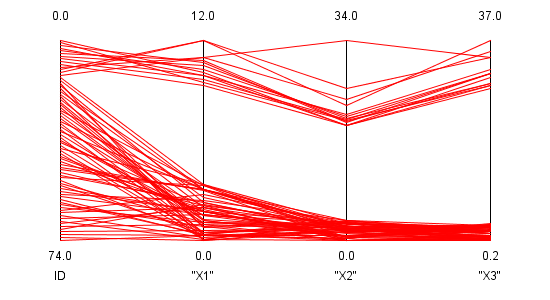
Abbildung 5: Darstellung des HBK-Datensatzes in Parallelen Koordinaten
Aus der Visualisierung des Datensatzes kann man sofort sehen, dass eine Gruppe von Datenpunkten klar vom
Rest der Daten abweicht. Aber dieses Verhalten kann nicht immer durch die Darstellung von hochdimensionalen Daten
festgestellt werden.
Daher ist es wichtig, ein verlässliches Maß berechnen
zu können, das angibt, ob Datenpunkte sich von der Mehrheit der Daten signifikant unterscheiden.
Um diese hochdimensionalen Ausreißer zu detektieren, wurde nun die Mahalanobis und die robuste Distanz berechnet
und in den Parallelen Koordinaten zusätzlich zu den Dimensionen des HBK-Datensatzes angezeigt. In Abbildung 6 werden
durch das Selektieren der größten Werte der Mahalanobis Distanz
auch "normale" Datenpunkte erfasst. Würde man allerdings nur den einen signifikanten Ausreißer, der von der
Mahalanobis Distanz angezeigt wird, auswählen, so würde man nicht alle Ausreißer detektieren.
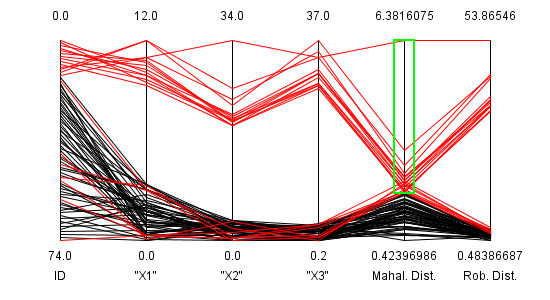
Abbildung 6: Selektion der Ausreißer mit Hilfe der Mahalanobis Distanz
Im Gegensatz dazu separiert die robuste Distanz alle Ausreißer klar vom Hauptteil der Daten, was in Abbildung 7 ersichtlich ist. Dabei ist es hilfreich, dass eine signifikante Lücke in den Werten der Distanzen auftritt.
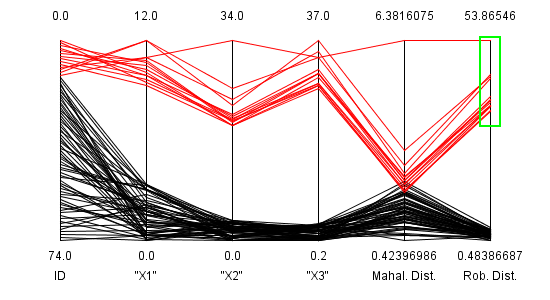
Abbildung 7: Selektion der Ausreißer mit Hilfe der Robusten Distanz
| « k means Clustering | Hauptkomponentenanalyse (PCA) » |