Beschreibung der Mahalanobis Distanz
Die Mahalanobis Distanz (Link zu Wikipedia-Artikel) gibt für jeden Datenpunkt an, wie weit dieser vom Zentrum der Daten (unter Berücksichtigung der Streuung) entfernt ist. Sie wird wie folgt berechnet:
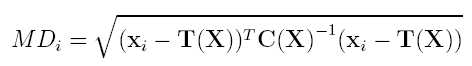
C(X) repräsentiert die Kovarianzmatrix und T(X) das komponentenweise arithmetische Mittel. Das heißt, dass die Mahalanobis Distanz wie die euklidische Distanz arbeitet, wobei allerdings die Streuung der Daten herausgerechnet und somit die Verteilung der Datenpunkte quasi normalisiert wird. Das folgende Beispiel soll dies demonstrieren.
Beispiel 1: Ausreißer-Erkennung in einer Punktwolke
Die Aufgabenstellung ist, die Punkte, die am weitesten vom Zentrum der Daten entfernt sind, als Ausreißer zu detektieren.
Dafür wird nun die Mahalanobis Distanz mit der euklidischen Distanz verglichen.
Mit diesem R Skript wurde dafür
ein Datensatz im CSV Format erstellt.
Das R Skript führt folgende Dinge aus:
- Es werden 1000 zweidimensionale Datenpunkte mittels Zufallsgenerator erstellt.
- Die x-Werte der Daten weisen eine Normalverteilung N(0,16) (Mittelwert 0, Varianz 16) auf.
- Die y-Werte der Daten weisen eine Normalverteilung N(0,1) auf.
- Für diese 1000 Datenpunkte wird die Euklidische Distanz und die Mahalanobis Distanz ermittelt.
- Für den zweiten Teil des Beispiels werden die Daten normalisiert, d.h. sowohl x- als auch y-Werte befinden sich im Intervalll [0, 1].
- Für die normalisierten Daten wird ebenfalls wieder die euklidische Distanz und die Mahalanobis Distanz berechnet.
- Am Ende werden sämtliche Daten in eine CSV-Datei exportiert.
Im ersten Teil des Beispiels werden die zweidimensionalen Datenpunkte in einem Scatterplot dargestellt, wobei
beide Achsen in der Visualisierung gleich lang sind. Dadurch erscheint die Punktwolke kreisförmig, obwohl sie aufgrund der unterschiedlichen
Wertebereiche auf den Achsen eigentlich elliptisch wäre.
In der ersten Abbildung werden die Datenpunkte mit hoher euklidischer Distanz eingefärbt. Dabei kann der auszuwählende Wertebereich
der euklidischen Distanz festgelegt werden:
- die oberen 25 % des Wertebereichs der euklidischen Distanz
- die oberen 50 % des Wertebereichs der euklidischen Distanz
- die oberen 75 % des Wertebereichs der euklidischen Distanz
- die oberen 90 % des Wertebereichs der euklidischen Distanz
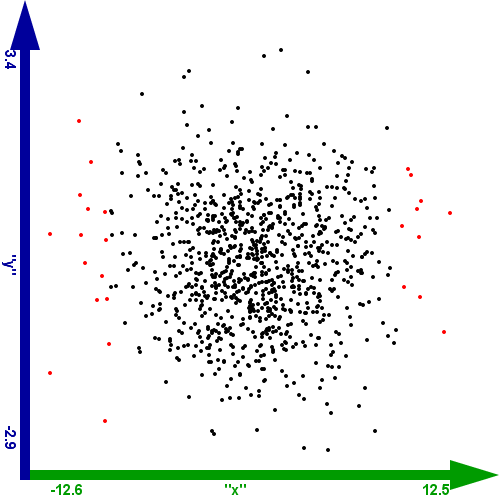
Abbildung 1: Selektion nach euklidischer Distanz (die oberen 25 % des Wertebereichs)
Man kann daraus ersehen, dass die euklidische Distanz hauptsächlich Datenpunkte ausschließt, die entlang
der X-Achse weit weg vom Zentrum liegen. Das ist dadurch begründet, dass der Wertebereich der
X-Achse viel größer ist. Somit ist die euklidische Distanz in diesem Fall ungeeignet, um Datenpunkte
am Rand der Punktwolke zu identifizieren.
Die selbe Vorgangsweise wurde mit der Mahalanobis Distanz vorgenommen. Dabei können
wieder folgende Selektionen gewählt werden:
- die oberen 25 % des Wertebereichs der Mahalanobis Distanz
- die oberen 50 % des Wertebereichs der Mahalanobis Distanz
- die oberen 75 % des Wertebereichs der Mahalanobis Distanz
- die oberen 90 % des Wertebereichs der Mahalanobis Distanz

Abbildung 2: Selektion nach Mahalanobis Distanz (die oberen 25 % des Wertebereichs)
Daraus kann man ersehen, dass die Mahalanobis Distanz besser geeignet ist, um
Datenpunkte, die weit weg vom Zentrum liegen zu identifizieren. Die Werte der X- und der Y-Achse werden gleich stark berücksichtigt,
obwohl sie unterschiedliche Wertebereiche aufweisen. Bei 90 % der selektierten Mahalanobis Distanzwerte zeigt sich, dass im Kern der Punktwolke
ein Kreis schwarz bleibt, anstatt einer Ellipse wie bei der euklidischen Distanz.
Eine ähnliche Funktionalität kann mit
der euklidischen Distanz erzielt werden, wenn die Werte auf allen Achsen auf ein einheitliches Intervall
(z.B. [0,1]) abgebildet werden. Allerdings streuen die Werte der Mahalanobis Distanz auch hier viel mehr als die der euklidische Distanz und man kann sie
daher als besseren Ausreißer-Detektor einstufen. Dies sieht man, in dem man die oberen 90 % des Wertebereichs der euklidischen Distanz auswählt,
wobei dann schon fast alle Datenpunkte selektiert sind.
- die oberen 25 % des Wertebereichs der euklidischen Distanz bei normalisierten Daten
- die oberen 50 % des Wertebereichs der euklidischen Distanz bei normalisierten Daten
- die oberen 75 % des Wertebereichs der euklidischen Distanz bei normalisierten Daten
- die oberen 90 % des Wertebereichs der euklidischen Distanz bei normalisierten Daten
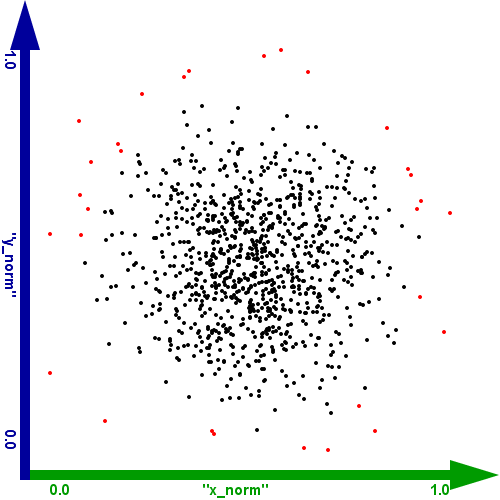
Abbildung 3: Selektion nach euklidischer Distanz von normalisierten Daten (die oberen 25 % des Wertebereichs)
Ein weiterer interessanter Vergleich zwischen den beiden Distanzen ergibt sich, wenn man die euklidische Distanz gegen die Mahalanobis Distanz im Scatterplot vergleicht. Wenn man die Distanzen der normalisierten Werte vergleicht, ergibt sich folgendes Bild:
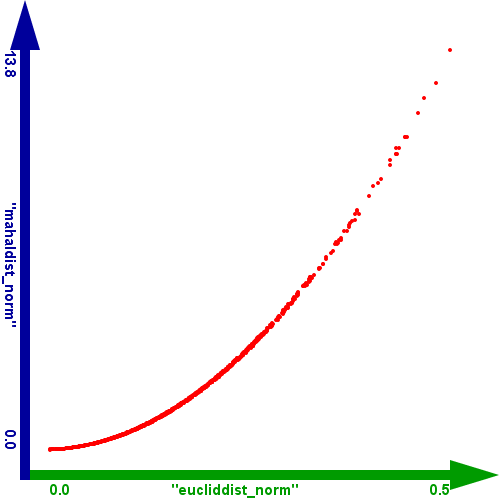
Abbildung 4: Vergleich zwischen der euklidischen Distanz und der Mahalanobis Distanz der normalisierten Werte.
Man kann daraus einen quadratischen Zusammenhang ableiten. D.h. die Funktionalität der beiden ist in diesem Fall gleich, wobei nur die Streuung der
Werte bzw. die Wertebereiche unterschiedlich sind.
Wenn man die beiden Distanzen allerdings auf den Original-Daten vergleicht so besteht kein Zusammenhang mehr. D.h. eine der Distanzen weist für
diese Aufgabenstellung die falschen Werte auf. (Wie oben erklärt ist dies die euklidische Distanz.)
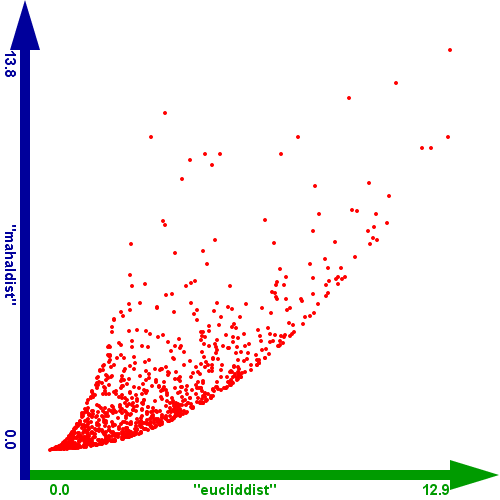
Abbildung 5: Vergleich zwischen der euklidischen Distanz und der Mahalanobis Distanz der Original-Werte.
Beispiel 2: Ausreißer-Erkennung in einer Punktwolke mit extremen Ausreißern
Da aber die Punkte oft nicht in einer Normalverteilung vorliegen und Messfehler Ergebnisse stark beeinflussen können,
wird in diesem Beispiel ein extremer Ausreißer auf der Y-Achse eingeführt.
Dafür wurde wiederum ein R Skript erstellt,
welches diesen Datensatz generiert.
Das Skript führt dabei folgende Schritte aus:
- Es werden 1000 zweidimensionale Datenpunkte mittels Zufallsgenerator erstellt.
- Die x-Werte der Daten weisen eine Normalverteilung N(0,16) (Mittelwert 0, Varianz 16) auf.
- Die y-Werte der Daten weisen eine Normalverteilung N(0,1) auf.
- Danach wird für den ersten Datensatz der y-Wert auf 17 gestellt.
- Die Daten werden wieder normalisiert, d.h. sowohl x- als auch y-Werte befinden sich im Intervall [0, 1].
- Für die normalisierten Daten werden wieder die euklidische Distanz und die Mahalanobis Distanz berechnet.
- Am Ende werden sämtliche Daten in eine CSV-Datei exportiert.
In der ersten Visualisierung zu diesem Beispiel werden alle 4 Größen (normalisierter x- und y-Wert, euklidische Distanz und Mahalanobis Distanz) in den parallelen Koordinaten gezeigt.
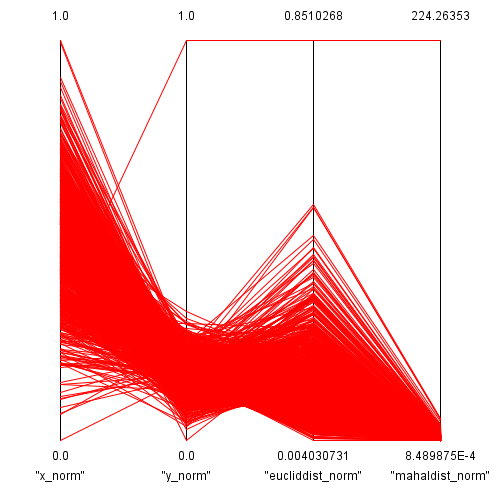
Abbildung 6: Ansicht des Datensatzes in den parallelen Koordinaten
Aus dieser Ansicht kann man bei den y-Werten bereits sehr schön den Ausreißer erkennen und man sieht wie er die Werte der anderen Datenpunkte
auf einen kleinen Ausschnitt des Wertebereichs nach der Normalisierung staucht. Man kann daraus auch erkennen, dass der Ausreißer sowohl mit der
euklidischen Distanz als auch mit der Mahalanobis Distanz sehr leicht identifiziert werden kann. Allerdings sieht man auch, dass sich die beiden Distanzen
für die restlichen Werte unterschiedlich verhalten. Die euklidische Distanz weist für die normalen Datenpunkte einen recht großen Datenbereich aus,
während die Mahalanobis Distanz einen kleinen Wertebereich für die "eigentlichen" Daten abdeckt.
Wie wirkt sich das nun auf die Ausreißer-Erkennung im Scatterplot aus? Dafür gehen wir wieder wie im ersten Beispiel vor:
- die oberen 25 % des Wertebereichs der euklidischen Distanz
- die oberen 50 % des Wertebereichs der euklidischen Distanz
- die oberen 75 % des Wertebereichs der euklidischen Distanz
- die oberen 90 % des Wertebereichs der euklidischen Distanz

Abbildung 7: Selektion nach euklidischer Distanz (die oberen 25 % des Wertebereichs)
Wenn man das obere Viertel des Wertebereichs der euklidischen Distanz auswählt, wo wird nur unser Ausreißer erkannt. Wählt man die
obere Hälfte des Wertebereichs aus, so werden bereits drei weitere Punkte der Punktwolke erkannt. Von nun an werden auch schon vermehrt
Datenpunkte der Punktwolke als Ausreißer detektiert.
Im Vergleich dazu tut sich bei der Mahalanobis Distanz sehr lange nichts. Wenn man bis zu 90 % des Datenbereichs auswählt, wird nur der
eine Ausreißer erkannt. Erst bei über 90 % werden dann weitere Datenpunkte der Punktwolke selektiert.
- die oberen 75 % des Wertebereichs der Mahalanobis Distanz
- mehr als die oberen 90 % des Wertebereichs der Mahalanobis Distanz
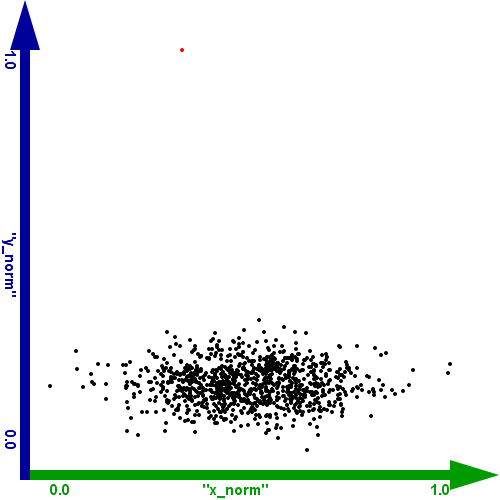
Abbildung 7: Selektion nach Mahalanobis Distanz (die oberen 75 % des Wertebereichs)
Nach dieser Analyse wäre für mich die euklidische Distanz in diesem Beispiel besser geeignet, um Ausreißer auch am Rande der Punktwolke
zu identifizieren, weil sie für die Daten in der Punktwolke einen größeren Wertebereich aufweist und man so leichter differenzieren kann.
Man sieht aber auch wie anfällig beide Distanz-Maße auf extreme Ausreißer sind. Sie können beide Distanz-Berechnungen so verfälschen, dass man nicht mehr
weiß, ob sie für die Aufgabenstellung brauchbar sind.
Daher ist es noch interessant sich anhand der Schätzung des Zentrums der Daten anzusehen, was der eine Ausreißer bewirkt. Das Zentrum der
Daten wird mit dem arithmetischen Mittel errechnet und fließt in die Berechnung beider Distanz-Maße ein. Das arithmetische Mittel der y-Werte
beträgt 0,16532. Würde man den Ausreißer nicht berücksichtigen so würde ein Mittelwert von 0,16448 errechnet werden. Da in diesem Datensatz mit
1000 Datenpunkten nur ein Ausreißer dabei ist, ist dessen Auswirkung noch relativ gering. Aber er bewirkt schon eine Änderung im Promille-Bereich
der Zentrums-Schätzung. Wenn das Verhältnis zwischen Ausreißern und normalen Datenpunkten sich weiter verschiebt, kann man sich vorstellen,
dass beide Distanz-Maße bei der Ausreißer-Detektion sowohl echte Ausreißer als auch "eigentliche" Datenpunkte als Ausreißer deklarieren.
Als Lösung dafür kann man eine robuste Schätzung für das Zentrum anwenden. Dafür würde sich beispielsweise das gestutzte arithmetische
Mittel oder der Median anbieten. Der Median für die Daten mit dem Ausreißer würde 0,16407174318621 betragen, während der Median ohne
Ausreißer 0,164071682214643 wäre. Man sieht daraus, dass erst an der 7. Kommastelle eine Änderung auftritt. Im Vergleich dazu
ergibt sich beim arithmetischen Mittel schon bei der 3. Kommastelle ein Unterschied.
Bei der Mahalanobis Distanz fließt außerdem auch die Streuung der Daten in der Form der Varianz mit ein. Diese beträgt mit Ausreißer
0,00312 und ohne Ausreißer 0,00243. Auch hier müsste eine robuste Schätzung angewandt werden.
Dies führt zur Berechnung der robusten Distanz, die ich allerdings in einem anderen Anwendungsfall besprechen will.
Warum berechnet man diese Distanzen?
Abschließend kann man sich noch die Frage stellen, warum man diese Distanzen berechnen muss, wenn man in der Visualisierung
den Ausreißer bzw. den Rand der Datenwolke klar identifizieren kann.
Bei hoch-dimensionalen Daten ist dies mit Visualisierungen leider nicht mehr so einfach, Ausreißer mit dem menschlichen Auge zu identifizieren.
Außerdem ist es hilfreich, ein Maß zu haben, welche die Ausreißer-Detektion automatisiert. Ansonsten müsste man Datenpunkte manuell auswählen.
Des weiteren haben die Beispiele gezeigt, dass die euklidische Distanz für die Ausreißer-Detektion nur dann brauchbar ist, wenn man
den Datenbereich aller Dimensionen zuvor normalisiert. Die Mahalanobis Distanz berücksichtigt die unterschiedlichen Wertebereiche automatisch,
ist aber noch anfälliger auf Ausreißer, als die euklidische Distanz.
Interessant wäre es noch herauszufinden, ob die euklidische Distanz mit normalisierten Wertebereich auch dann so effektiv ist, wenn die
Punktwolke nicht entlang der X- oder Y-Achse gestreckt wäre, sondern diagonal liegen würde.
Referenzen
Die Mahalanobis Distanz wird derzeit auf folgenden Seiten referenziert:
|
|
Visualisierung - Statistische Analysen mit Parallelen Koordinaten
(Wintersemester 2005/06) |